早期控制絲狀菌污泥膨脹(簡稱污泥膨脹)的主要手段是投加藥劑殺死絲狀菌,或投加混凝劑和助凝劑以增加污泥絮體的比重[1],但這些方法往往無法徹底解決污泥膨脹問題,相反地可能會帶來出水水質惡化的不良后果。其后人們逐漸認識到,活性污泥中的菌膠團細菌和絲狀菌構成一個共生的微生物生態體系,在這種共生關系中,絲狀菌是不可缺少的重要微生物,對于高效、穩定地凈化污水起著重要作用,并逐漸地從簡單殺死絲狀菌過渡到利用曝氣池中的生長環境調整絲狀菌的比例,從而達到控制污泥膨脹的發生即進入環境調控階段。環境調控概念的使用是人們在污泥膨脹控制技術和實踐上的一大進步,其主要出發點是使曝氣池中的生態環境有利于選擇性地發展菌膠團細菌,利用生物競爭機制抑制絲狀菌的過度生長和繁殖,將絲狀菌數量控制在一個合理的范圍之內,從而控制污泥膨脹的發生和發展,同時利用絲狀菌的特性凈化污水,穩定處理工藝。近年來選擇器理論得到充分的發展和應用就是這一概念的具體體現。
1 污泥膨脹理論的統一
活性污泥是一混合培養系統,其中至少存在著30種可能引起污泥膨脹的絲狀菌。在絲狀菌與菌膠團細菌平衡生長時不會產生污泥膨脹問題,只有當絲狀菌生長超過菌膠團細菌時,才會出現污泥膨脹。絲狀菌和菌膠團細菌的生理和生化性質差異見表1。
|
通過近年來國內外對活性污泥膨脹問題研究進展的分析和綜合,可以將引起絲狀菌污泥膨脹的原因分為5種類型,即a.基質限制;b.DO限制;c.營養物缺乏;d.pH影響;e.H2S影響[2]。
1.1 廣義Monod方程
絲狀菌與菌膠團細菌競爭的數學模型遵循多種基質限制的廣義Monod方程,即MonodMcGee方程[1]:
μ=μmax(S1/K1+S1)(S2/K2+S2)…(Sn/Kn+Sn) (1)
式中μmax——最大生長速率,d-1
Ki——第i種基質親和力,mg/L
Si——第i種基質濃度
根據式(1)可知,基質限制、DO限制和營養物缺乏型的污泥膨脹問題都可用廣義Monod方程來加以解釋(當氮嚴重缺乏時的污泥膨脹不能歸入這一理論,原因在于若缺乏氮,微生物便不能充分利用碳源合成細胞物質,過量的碳源將被轉變為多糖類胞外貯存物,這種貯存物是高度親水型化合物,易形成結合水,影響污泥的沉降性能,從而產生高粘性膨脹,其不屬于絲狀菌污泥膨脹范疇)。
關于pH的影響,可在動力學方程參數的基礎上,以動力學常數的乘積因子的形式進行耦合,或者單獨列出其動力學方程,從而統一在廣義Monod方程之下。關于H2S的影響,文獻報道引起污泥膨脹的H2S濃度很低,一般是在1~2.0 mg/L。但通過向污水中添加H2S的試驗發現,即使H2S濃度達到 50 mg/L也不會發生污泥膨脹。事實上,一些厭氧裝置雖然出水含有大量H2S,但是揮發性有機酸濃度很低時,好氧后處理也不發生污泥膨脹;當揮發性有機酸達到一定濃度時需引起注意,其中主要的低分子有機酸(乙酸、丙酸)易于降解,因此造成耗氧速率的增加[3],引起氧的限制型膨脹,這是造成污泥膨脹的根本原因。而H2S的出現是污水厭氧發酵的一個伴隨現象,也可歸為DO限制型的膨脹,從而廣義的Monod動力學模型可以在一定程度上很好地統一污泥膨脹的理論。
1.2雙基質Monod方程
由于城市污水中N、P和其他營養元素一般不缺乏,因此在一般情況下,可只考慮碳源限制和DO限制兩種情況。這樣,城市污水的絲狀菌污泥膨脹問題就簡化為兩種主要類型,即基質限制和DO限制型。
μ=μmax(S/KS+S)·(DO/KDO+DO)(2)
式中μmax ——最大生長速率,d-1
KS——基質親和力,mg/L
KDO——DO親和力,mg/L
2 污泥膨脹數學模型的研究
為了簡化系統模型,假設:①活性污泥由兩大類微生物群組成,即絲狀菌和菌膠團菌;②微生物生長主要受到碳源和DO限制;③微生物生長的動力學可用同一基本模型來描述;
④曝氣池是完全混合式。模型所描述的系統如圖1所示。
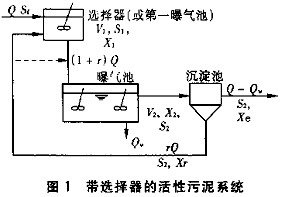
其中反應器1根據不同的試驗目的,可以分別是選擇器、曝氣池等,反應器2是曝氣池。在沒有選擇器的系統中,回流污泥按虛線所示的途徑回流。根據以上假設及圖1中的物料平衡關系,可給出選擇器和曝氣池中基質(碳源和DO)和微生物(菌膠團和絲狀菌)的一組方程。
選擇器中菌膠團菌:
dX11/dt=(μ1-kd1-1/θc)X11 (3)
絲狀菌:
dX21/dt=(μ2-kd2-1/θc)X21(4)
碳源基質:
dS11/dt=Dk(S10+rS12)-(1+r)·D1S11-μ1X11/Y1-μ2X21/Y2 (5)
DO:
dS21/dt=-(1+r)D1S21+Kla(S2S-S21)-μ1X11/Y1-μ2X21/Y2 (6)
曝氣池中菌膠團菌:
dX12/dt=(1+r)D2(X11-X12)+(μ1-kd1)X12 (7)
dX22/dt=(1+r)D2(X21-X22)+(μ1-kd1)X22 (8)
dS12/dt=(1+r)D2(S11-S12)-μ1X12/Y1-μ2X22/Y2(9)
dS22/dt=(1+r)D2(S21-S22)+Kla(S2S-S22)-μ1X12/Y1-μ2X22/Y2(10)
式中
狀態變量:
Xik——污泥濃度,mg/L;其中i=1或2,1表示菌膠團菌,2表示絲狀菌;k=1或2,1表示選擇器,2表示曝氣池
Sjk——基質濃度,mg/L;其中j=1或2,1表示碳源,2表示DO
S10——碳源基質初始濃度,mg/L
S2S——飽和DO濃度,mg/L
操作變量:
Dk——稀釋率,d-1
r——回流比
動力學常數:
kdi——衰減常數,d-1
Yi——產率系數,g/g
Kla——傳質系數,min-1;其常數見表1
μi——比生長速率
2.1進水負荷和曝氣強度的影響
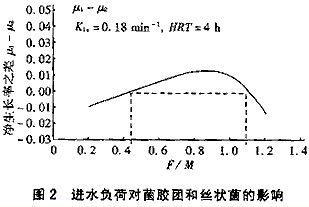
從圖2可見,絲狀菌和菌膠團細菌的競爭優勢隨進水負荷而變化。低負荷階段[<0.4kgCOD/(kgMLSS·d)],DO的供應充分,出現基質限制的情況;高負荷階段[>1.1kgCOD/(kgMLSS·d)],基質濃度比較高,出現DO限制的情況;而在中間負荷范圍內,絲狀菌與菌膠團菌處于合理的比例,系統不發生污泥膨脹。
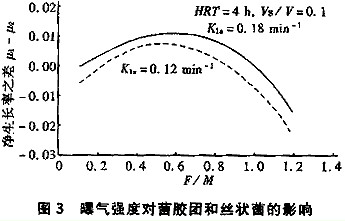
圖3表明,即使存在選擇器,低負荷和高負荷階段仍然會發生污泥膨脹,其限界值與沒有選擇器的系統不同。對于高負荷系統,曝氣強度大可以提高污泥膨脹發生的上限,同樣低負荷系統發生膨脹的下限也降低。對于中間負荷階段,如果供氧不充分,絲狀菌仍有可能大量繁殖并形成污泥膨脹。對于不同的曝氣強度,兩種微生物競爭優勢發生轉變的限界值是不同的,這就是雙基質動力學方程與傳統的單一碳源基質限制動力學方程描述污泥膨脹現象的本質區別。試驗的結果也表明,完全混合曝氣池在不同負荷下維持穩定的沉降性能所需要的DO濃度是不一樣的,而不是象文獻報道的維持在固定的1.0~2.0 mg/L之間[1]。
2.2進水流量和濃度變化的影響
試驗發現在停留時間分別為3、4、5 h時,系統的DO濃度分別為1.2、2.2、3.0 mg/L。圖4是流量和基質濃度增加1.5倍時采用計算機模擬的結果。
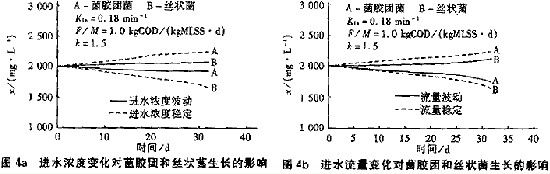
在穩定的流量和濃度條件下長期運行的結果是菌膠團細菌占優勢,而流量或基質濃度的變化會造成絲狀菌的過度生長,且絲狀菌的生長不是一簡單的可逆過程,會造成污泥沉降性能的改變。上述結果是在相對高的負荷下的模擬結果,低負荷下的結論相反。
3 結論
①通過分析,將絲狀菌污泥膨脹概括為5種類型,即:低基質濃度、低DO、營養物(N、P)缺乏、H2S影響和pH引起的膨脹。采用廣義Monod方程可解釋大部分類型的污泥膨脹問題,這在一定程度上統一了污泥膨脹理論。由于城市污水中N、P和其他營養元素一般不缺乏,因此在一般情況下,只考慮碳源和DO限制兩種情況。
②在雙基質限制下,低負荷的完全混合曝氣池不利于污泥沉淀性能的改善,但中、高負荷下的污泥膨脹則在完全混合曝氣池中有所緩解。對于中、高負荷系統,由于首端缺氧對污泥沉降不利,所以在推流式曝氣池需采取措施避免供氧不足;反之,推流式曝氣池有利于克服低負荷的污泥膨脹,即高負荷與低負荷是兩種類型完全相反的污泥膨脹現象。
③對活性污泥膨脹,既要從宏觀角度考慮,也要從微觀角度去考慮。就活性污泥工藝的運轉條件而言,負荷、基質濃度和DO濃度的水平是宏觀條件,但曝氣池首端的實際負荷、基質濃度和DO濃度是更為重要的因素,后者是決定污泥膨脹的微環境,種群的動態是由其微環境中的營養物條件所決定的。
④傳統的選擇器僅僅考慮低基質濃度型污泥膨脹。選擇器是在完全混合或推流曝氣池前加一個停留時間非常短(15 min)的小池,在選擇器內利用兩類細菌不同的生長速率選擇性地培養和發展菌膠團細菌,使其成為曝氣池中的優勢菌。在以上的理論分析和研究的基礎上,可以對選擇器的概念進行擴展。廣義的選擇器可以包括低DO型污泥膨脹,可采用不同的選擇器的形式如再生池和強化曝氣池等方法,恢復菌膠團細菌的降解能力、提高供氧能力和降低負荷以控制高負荷型的污泥膨脹。來源:中華環保互聯網


